WHAT IS THE BIG O NOTATION?
Big O notation is a mathematical notation that describes the limiting behaviour of a function when the argument tends towards a particular value or infinity. It is a member of a family of notations invented by Paul Bachmann, Edmund Landau, and others, collectively called Bachmann–Landau notation or asymptotic notation.
WHY SHOULD YOU CARE?
For a small app that processes little data, such analysis might be unnecessary. This is because the difference in the runtime of algorithms might have little impact on your app. For large applications that manipulate a large amount of data, this analysis is crucial. Because inefficient algorithms will create a significant impact on the processing time. With a good knowledge of Big-O notation, you can design algorithms for efficiency. Thus, you'll build apps that scale and save yourself a lot of potential headaches.
For your coding interviews. Yeah, you heard me right. You are likely to get asked by an interviewer the runtime complexity of your solution. So it's good to have an understanding of the Big O notation. the best way to understand Big O thoroughly was to produce some examples in code.
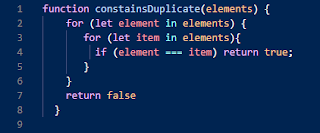
O(n^2 ) - Quadratic Runtime
O(n^2 ) denotes an algorithm whose runtime is directly proportional to the square of the size of the input data set. An example of this is a nested iteration or loop to check if the data set contains duplicates.
Deeper nested iterations will produce runtime complexities of O(n^3 ), O(n^4 ) etc.
LINEAR SEARCH VS BINARY SEARCH
A linear search is also known as a sequential search that simply scans each element at a time. Suppose we want to search an element in an array or list; we simply calculate its length and do not jump at any item.
Searching in a small list
Let's say we have a list of 7 items
We want to check if number 5 is in the list. We would utilize both linear and binary search
Linear Search
With linear search, we go through the list sequentially until we find what we are looking for. So, it'd be similar to this
if we were dealing with the first 1000 primes, the time complexity would quickly rise because of the straight-line graph linear search plots. Below is an image of the straight-line linear search plots vs that of binary search.
Even if you don't understand BigO notation, you can clearly see that linear search keeps going straight up at approximately 45 degrees as the number of search terms increase.
Binary Search
With binary search, we use the mean of the highest and lowest numbers of the considered set. The list has to be ordered for binary-search to work.
How it works
Binary search repeatedly divides the array into halves and computes the average until it lands on the item being search. Let's say we are looking for number 32 in the first 50 whole numbers. We would work through this in pseudocode
The pseudocode is a simplified representation.
comparing linear and binary
In this array of 50 items. Linear search would perform a maximum of 50 'guesses' while binary search won't perform more than 6 (log to base 2 of 50). In our pseudocode above, we only needed 3
Here's the code for binary search. We are still using our array of first 7 primes.
COMPARING THE EFFICIENCY OF LINEAR AND BINARY SEARCH
- Input data needs to be sorted in Binary Search and not in Linear Search
- Linear search does the sequential access whereas Binary search access data randomly.
- Time complexity of linear search -O(n) , Binary search has time complexity O(log n).
- Linear search performs equality comparisons and Binary search performs ordering comparisons
WHY IS ANY OF THIS IMPORTANT
The speed of your software depends on the execution speed of your algorithms. To deliver high-quality software, you have to know the right algorithm for the job. You don't want to keep your users waiting for 10 seconds when the wait time could be less.
SO WHAT IS A FIBONACCI?
The Fibonacci sequence is the integer sequence where the first two terms are 0 and 1. After that, the next term is defined as the sum of the previous two terms.
Probably one of the most famous algorithms ever, but still lot of people struggles when trying to find an efficient solution. Let me introduce you to the Fibonacci sequence.
Statement
Given a number N return the index value of the Fibonacci sequence, where the sequence is:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...
After a quick look, you can easily notice that the pattern of the sequence is that each value is the sum of the 2 previous values, that means that for N=5 → 2+3 or in maths:
F(n) = F(n-1) + F(n-2)
First implementation
So let’s go directly to the first implementation, we are gonna use a simple loop to achieve our solution.
This is probably the first solution that will come to your mind. The important part here is that we calculate the next number by adding the current number to the old number.
And the good news is that has a O(n) time complexity. Fair enough for the first try right? But let’s try to see some other ways to approach the problem.
Recursive solution
Now let’s see if we can make it look fancier, now we will use recursion to do that.
Easy right? we just solved the problem in 2 lines of code, but let’s take a deeper look and see what’s actually happening.
Base case: we just need to check if the value is less than zero for return the 2 firsts cases.
But now the bad news… We have increased the time complexity of our algorithm almost to the worst case. If you take a look at the graphic, you will see the orange color (2^N) time complexity, which means that our current implementation is exponential…
Memoization
Finally, and following the recursive approach we will use memoization to improve our efficiency, but first of all, what’s memoization? as Wikipedia says:
Is an optimization technique used primarily to speed up computer programs by storing the results of expensive function calls.
What does that means and why should we take care about that in our implementation? Basically, if we just store the value of each index in a hash, we will avoid the computational time of that value for the next N times.
This change will increase the space complexity of our new algorithm to O(n) but will dramatically decrease the time complexity to 2N which will resolve to linear time since 2 is a constant.
Conclusion
This was just an example of how to design, improve and analyze an algorithm, in this case it was the Fibonacci sequence, which is simple enough to understand and surprising to see the performance boost we achieved just with some small changes.











Comments
Post a Comment